Spherical Co-ordinate System

http://mathworld.wolfram.com/SphericalCoordinates.html




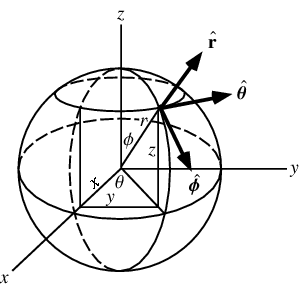
1. Curvilinear co-ordinates

2. Used for describing positions on a sphere or spheroid

3. Denoted as set (r,    (azimuthal angle),  (polar angle) ) 


4.  

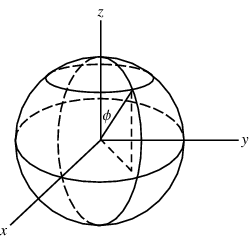
In spherical coordinates, the polar angle is the angle measured from the -axis, denoted  in this work, and also variously known as the zenith angle and colatitude. ,

  ( where  is the latitude) from the positive z-axis with 

5. It is a logical extension of the usual polar coordinates notation, with 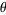 remaining the angle in the 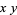-plane and  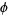becoming the angle out of that plane.

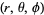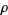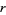6. The symbol  is sometimes also used in place of , and  and 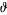 instead of . 

7. The spherical coordinates  are related to the Cartesian coordinates  by

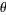			(1)
			(2)

where 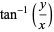, , 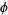and , and the inverse tangent must be suitably defined to take the correct quadrant of 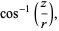 into account.

8. In terms of Cartesian coordinates,

			(4)
			(5)

9. The line element is

(13)

the area element

(14)

and the volume element

http://en.wikipedia.org/wiki/Spherical_coordinate_system 10.  In geography and astronomy, the elevation and azimuth (or quantities very close to them) are called the latitude and longitude, respectively; and the radial distance is usually replaced by an altitude (measured from a central point or from a sea level surface). 11. Spherical coordinates are useful in analyzing systems that have some degree of symmetry about a point, such as volume integrals inside a sphere, the potential energy field surrounding a concentrated mass or charge, or global weather simulation in a planet's atmosphere. A sphere that has the Cartesian equation x2 + y2 + z2 = c2 has the simple equation r = c in spherical coordinates. 12.