Fundamental Loop Matrix

Sources:

http://www.transtutors.com/homework-help/Networks+%26+Systems/Network+Graph+Theories/loop-matrix-question.aspx

http://books.google.com/books?id=9c38IdqCbusC&pg=PA1119&lpg=PA1119&dq=define+fundamental+loop+matrix&source=bl&ots=63Jwqa6QEH&sig=Rqp4AG4sbnI5_eeyaVdgp_DK6AE&hl=en&ei=lfoiTaGdNo3KrAft56D-Cw&sa=X&oi=book_result&ct=result&resnum=5&ved=0CCEQ6AEwBA#v=onepage&q=define%20fundamental%20loop%20matrix&f=false

http://www.transtutors.com/homework-help/Networks+%26+Systems/Network+Graph+Theories/loop-matrix-question.aspx

Definition:

Consider a connected graph G with b branches and n_t nodes. Select any arbitrary tree. The tree will contain n = n_t - 1 tree branches (twigs) and l = (b - n) link branches. Every link defines a fundamental loop of the network. Let us take the example of the graph shown in Fig. a.

                    

                                              Fig.

Let T be a tree of G as shown in Fig. b. The number of fundamental loops of this graph will be (b - n) = 3. the three f-loop l₁, l₂ and l₃ are shown in Fig. c. In order to apply KVL to each fundamental loop, we take reference direction of the loop which coincides with the reference direction of the link defining the loop.

   l₁ : v₁ + v₂ + v₅ + = 0 

   l₂ : v₂ + v₃ + v₄ = 0 

   l_{3 :} v_{1 +} v_{3 +} v₆ = 0

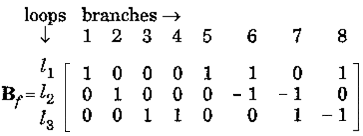
In matrix form, we can write

B_f v_b = 0   (KVL)    

Where  is an  matrix called the fundamental loop matrix or tie-set matrix

    B_f = [b_kj]

Where b_kj are the elements of b_f the (k,j) element of the matrix is defined as follows:

   b_kj = 1 when branch b_j is in the f-loop l_k and their reference directions (orientations) coincide

   b_kj = -1 when branch b_j is in the f-loop l_k and has opposite orientation

   b_kj = 0 when branch is not in the f-loop

Example:

In the graph shown in Fig. a tree consisting of branches 4, 5, 6, 7, 8 is chosen, as shown by heavy lines. Write the fundamental loop matrix of the graph.

SOLUTION

The fundamental loops defined by links {1, 2, 3} and their orientations are shown in Figs, c and d. Consider loop l₁. It contains branches {1, 6, 8, 5}. The orientation of loop l₁ is given the same orientation as its defining link 1. Therefore the element b₁₁ is written 1. The directions of branches 6, 8 and 5 in l₁ are the same as l₁. therefore the entries
          
                      
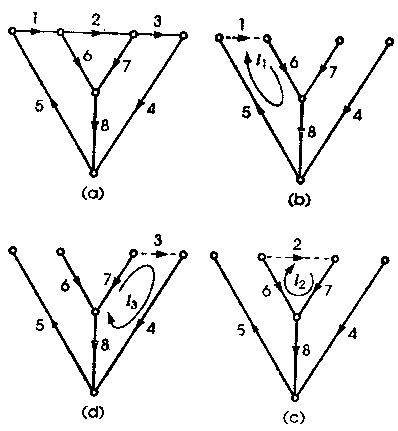
FIG. 

b₁₆,b₁₈  and b₁₅  are each equal to 1. Since branches 2, 3, 4 and 7 are not in loop b₁₃ = 0,b₁₄ = 0,b₁₇ = 0.

Loop l₂ contains branches {2, 6, 7}. The orientation of l₂ is given the same orientation as its defining link. 2. Therefore the element b₂₂ = 1. The orientations of branches 6 and 7 are opposite to the orientation of l₂ consequently, b₁₂₆ = -1 and b₂₇ = -1 Since branches {1, 3, 4, 5, 8} are not contained in l₂, b₂₁ = 0,b₂₃ = 0,b₂₄ = 0,b₂₅ = 0,b₂₈  = 0.

Loop l₃ has branches (3, 4, 8, 7). The orientation of l₃ is the same as that of its defining link 3.Therefore the element b₃₃ = 1 The directions of branches 4 and 7 coincide with the orientation of l₃ Hence b₃₄ = 1, b₃₇ = 1. The orientation of branch 8 does not coincide with the orientation of l₃. Hence b₃₈ = -1. Since branches {1, 2, 5, 6} are not contained in l₃,b₃₁ = 0, b₃₂ = 0, b₃₅ = 0, b₃₆ = 0. Thus, we obtain the following matrix: