Use of multi-dimensional arrays in C/C++ is a little tricky especially after 2+ scale.
I have devised some tips to understand them better:
For a n-scale array, to calculate offset address for a particular element, use the formula:
Base address of array + 2(pow n-1) * (size of data type) (nth index) + 2(pow n-2) * (size of data type) (n-1th index) till n is 1 + (size of data type) * last entryindex.
discussing scale 4:
i j k l
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
For example, for second last entry, put values as:
BA + 2 (pow 4-1)* sizeof DT *(1) + 2(pow 2) * sizeof DT *(1) + 2(pow 1) * sizeof DT *(1) + sizeof DT *0
Tip 2:
To completely dereference a data value, total de-reference operators must be equal to the scale of array.
Tip 3:
(arr + index) = &(arr[index) at any level.
Keeping these tips in mind, i have solved a complex code available at:
http://pastie.org/1053208
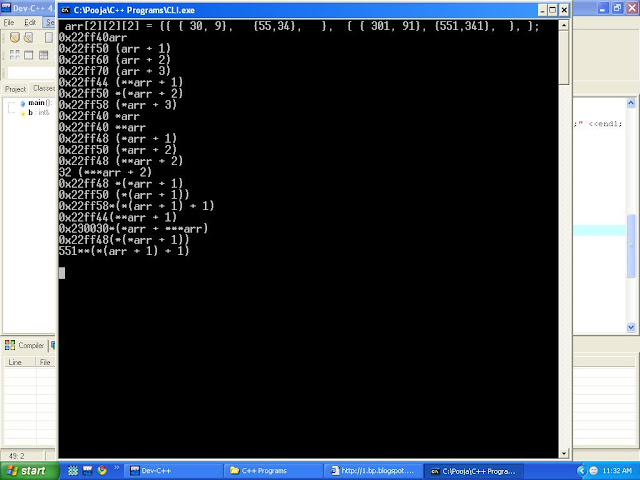
Output as seen on GNU compiler is pasted below:
Feel free to post multi-dimensional arrays questions in C/C++
I have devised some tips to understand them better:
For a n-scale array, to calculate offset address for a particular element, use the formula:
Base address of array + 2(pow n-1) * (size of data type) (nth index) + 2(pow n-2) * (size of data type) (n-1th index) till n is 1 + (size of data type) * last entryindex.
discussing scale 4:
i j k l
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
For example, for second last entry, put values as:
BA + 2 (pow 4-1)* sizeof DT *(1) + 2(pow 2) * sizeof DT *(1) + 2(pow 1) * sizeof DT *(1) + sizeof DT *0
Tip 2:
To completely dereference a data value, total de-reference operators must be equal to the scale of array.
Tip 3:
(arr + index) = &(arr[index) at any level.
Keeping these tips in mind, i have solved a complex code available at:
http://pastie.org/1053208
5 comments:
How would you compute the offset of an element in an array which is variably-dimensional. Consider a variably-dimensioned 2-scale array as,
0 1 2 3 4 5
0 1 2
0 1 2 3 4
0 1 2 3 4 5 6 7 8 9
How about a variable-dimensioned 3-scale array?
All the index of the multi-dimensional array should be defined for the base offset calculation using mentioned formula
Did you expect such an easy question? :D
Well, how would you compute the offset in the array is being worked upon. Say, after a few manipulations the (above) array becomes,
0 1 2 3
0 1 2 3 4 5
0 1 2 3 4
0 1 2 3 4
0 1 2 3 4 5
Maintaining the indices/length of each array would be an overhead in case the array is not growing. Thoughts?
Is there an easy implementation that will result in very fast access to a given element. Think of a best-time implementation for such a variable-array class with the following methods:
public Object get(int index);
public Object peek();
public void set(Object value, int afterIndex);
public void push(Object value);
Amiable brief and this fill someone in on helped me alot in my college assignement. Thanks you on your information.
0x22ff10 **arr
0x22ff18 (*arr + 1)
0x22ff20 (*arr + 2)
0x22ff18 (**arr + 2)
32 (***arr + 2)
0x22ff18 *(*arr + 1)
0x22ff20 (*(arr + 1))
0x22ff28*(*(arr + 1) + 1)
0x22ff14(**arr + 1)
0x230000*(*arr + ***arr)
0x22ff18(*(*arr + 1))
551**(*(arr + 1) + 1)
0x22ff20 arr[1]
0x22ff20 arr[1][0]
0x22ff20 arr[1][]
0x22ff20 arr[0][1]
0x22ff20 arr[1][][]
0x22ff20 arr[0][1][]
0x22ff14&arr[0][0][1]
0x22ff24&arr[1][0][1]
9arr[0][0][1]
91arr[1][0][1]
Display using sizeof operator
32 sizeof arr
16 sizeof *arr
8 sizeof **arr
4 sizeof ***arr
4 sizeof (arr + 1)
4 sizeof (*arr + 1)
4 sizeof (**arr + 1)
4 sizeof (arr + 2)
4 sizeof (*arr + 2)
4 sizeof (arr + 3)
4 sizeof (*arr + 3)
8 sizeof *(*arr + 2)
4 sizeof (**arr + 2)
4 sizeof (***arr + 2)
8 sizeof *(*arr + 1)
16 sizeof (*(arr + 1))
8 sizeof *(*(arr + 1) + 1)
4 sizeof (**arr + 1)
8 sizeof *(*arr + ***arr)
8 sizeof (*(*arr + 1))
4 sizeof **(*(arr + 1) + 1)
For a variable array class, binary tree storage will work best, need to think more
Post a Comment